1，平面解析几何：

所谓平面解析几何，就是利用函数的方式解决平面几何问题，也就是利用坐标去解决几何问题。

前面我们讲向量和立体几何时都发现了，利用坐标去解决几何问题比直接使用几何方法去解决几何问题要简单很多，因为一切用数据说话，不需要提前找到位置或方位。

2，直线的方程：

直线对应的函数我们初中已经学过了，就是一次函数，其解析式为y=kx+b。

其实，这个y=kx+b叫做直线的斜截式，因为它直接体现出的是直线的斜率与y轴截距。

除了这个解析式之外，直线还有很多形式的解析式。

比如：y-b=k（x-a），这是直线的点斜式，因为它直接体现出的是直线的斜率与直线所过的一个点（a,b）。

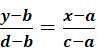
这是直线的两点式，因为它直接体现出的是直线说过的两个点（a,b），（c,d）。

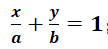
这是直线的截距式，因为它直接体现出的是直线在x轴上的截距a和在y轴上的截距b。

最后，Ax+By+C=0叫做直线的一般方程，它与后面我们要讲的关于直线的公式有关。

这些各种形式的直线方程不需要都记住，大家只要把我们最熟悉的斜截式记住就可以了，其它的只是在给出条件对应时可以直接写方程，但是不会也不会影响我们做出这道题来。

3，斜率与倾斜角：

我们刚才一直在提斜率这个概念，那么什么是斜率呢？

斜率就是倾斜角的正切值。

那么倾斜角又是什么呢？

倾斜角就是直线与x轴正半轴的夹角。

倾斜角的取值范围为[0°，180°）。

有一个常考易错题，（1）倾斜角与斜率是不是一一对应关系？（2）是不是每个倾斜角都有斜率？（3）是不是每个斜率都对应有倾斜角？

这里面，（1）和（2）是错误的，（3）是正确的。

原因就在最特别的角90°上，因为90°是没有正切值的，因此90°的倾斜角是没有斜率的。

4，用斜率证明平行与垂直：

这个很多初中已经给学生补充了，因为中考二次函数大题是可以使用的。

如果两个直线斜率相等，那么它们就是平行关系。

当然，如果两个直线都没有斜率，它们也是平行关系。

如果两个直线的斜率的乘积为-1，那么它们就是垂直关系。

当然，如果两个直线一个斜率为0，另一个没有斜率，它们也是垂直关系。

证明垂直的方法一定要和向量证明垂直的方法区分开，斜率相乘等于-1是垂直，向量乘积为0是垂直。

5，直线相关公式：

（1）两点间斜率公式：两点坐标P（a,b），Q（c,d）（a≠c），则直线斜率为：

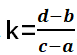
（2）两点之间距离公式：还是上述两点，他们之间的距离为：

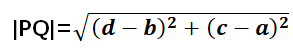
这两个公式是在坐标系中构建直角三角形得到的。

（3）点到直线的距离公式：点P（a,b）到直线l：Ax+By+C=0的距离为：

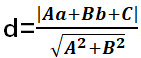
（4）两平行线之间距离公式：两条平行线Ax+By+C=0与Ax+By+D=0（C≠D）的距离为：

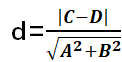
这两个公式是通过直线的一般方程完成的。

特别注意两平行直线距离公式，一定先把两平行直线的x与y前系数化为一样的之后再套公式。

6，对称问题：

（1）点关于点对称问题：

例1，求点（2,4）关于点（3,-1）的对称点坐标？

这个问题可以设出所求点坐标，然后利用对称点坐标等于两点坐标之和除以2求出对称点坐标。

还有一种办法，就是看距离。

比如这道题，被对称点的横坐标为2，比对称点的横坐标3小1，因此所求点的横坐标就比对称点的横坐标大1为4；被对称点的纵坐标为4，比对称点的纵坐标-1大5，因此所求点的纵坐标就比对称点的纵坐标小5为-6。

所以，所求对称点坐标为（4，-6）。

（2）线关于点对称问题：

例2：求直线6x+y=6关于点（1,2）的对称直线方程？

首先明确，两条线如果关于一个点对称，那么这两条线一定是平行关系，也就是斜率相等。

另外，两条线关于一个点对称，那么它们上的所有点都是关于这个点对称的关系。

所以，求这条对称直线方程，可以先设出斜率来，然后从已知直线上随便找一个出来，求出其关于对称点对称的点的坐标代入所求直线中，就可以把所求直线求出来了。

比如这道题，可以先设出所求直线方程为6x+y=t，然后从已知直线上找到点（1,0）。

（1,0）关于（1,2）对称的点的坐标为（1,4），代入所设方程中，解得t=10。

因此，所求直线方程为6x+y=10。

（3）点关于线对称问题：

例3：求点（1,2）关于直线6x+y=6的对称点坐标？

如果两个点关于一条直线对称，那么这两个点的连线一定与对称轴垂直，且这两个点的中点一定在对称轴上。

我们就利用这两点，设出所有点坐标，列出方程组求解即可。

比如这道题，我们可以设出做求点坐标为（a,b）。

根据两点连线与对称轴垂直可以列出方程：[（b-2）/（a-1）]*（-6）=-1；

根据两点中点在对称轴上可以列出方程：6*[（a+1）/2]+（b+2）/2=6。

联立解方程组即可解出所求点为（13/37，70/37）。

（4）相交直线对称问题：

例4：求直线6x+y=6关于直线3x-y+4=0的对称直线方程？

求关于某条直线对称的一条直线的对称直线方程。

首先，这三条直线一定交于一个点，先通过两条已知直线把这个点求出来。

然后，从被对称直线上任取一点，求出它关于对称轴的对称点。

交点和求出的对称点都在所求直线上，两点确定一条直线，所求直线就求出来了。